|
|
|
|
|
|
|
| . . Homepage. . . . What We've Been Up To. . . . About Me & Al. . . . Teddington. . . . Pictures. . . . Puzzles. . . . Puzzles Too. . . . Music. . . . Misc. . . . My Films. . . . Credits etc. . |
|
||||
|
|
||||
|
Tetrominoes Five Easy Pieces? The forgotten faces of polyforms... Every serious puzzler or recreational mathematician will have a set of pentominoes, the 12 shapes made by connecting 5 squares, whole edge to whole edge in all possible ways. However, the wide and ever-growing variety of pentomino puzzles often cause the tetrominoes to be forgotten. The five tetrominoes are made from 4 squares, touching whole edge to edge. I will show here that there are challenging puzzles to be found using these neglected pieces.
Sadly, these five shapes will not fit together, as you might initially try, to form a 4x5 rectangle. This can be readily seen from the fact that if you chequer the 5 pieces, alternately black and white, you will see that the T piece has 3 squares of one colour and one of the other, whereas all the others have two of each. A chequered 4x5 rectangle would have equal numbers of each. Therefore we can also rule out a 10x2 rectangle for the same reason. Sad but true... This means that the only shapes which can be formed from the five pieces will have an unequal number of blacks and whites when chequered.
This is one such shape (above), which has seven solutions. Another rectangle which doesn't work is a 7x3 with a central space. The chequering test works OK, but the pieces just won't fit. Leaving a space one unit to the left (or right) of centre yields 4 solutions. Another 4 solutions can be found by leaving a space at the end of the central line. A further three solutions are found by leaving a space one unit in from a corner, along the longer side. A final two solutions exist if the space is in the centre of the top or bottom row. Note that these duplications occur due to lateral or rotational symmetry. The following table summarises these possibilities. Any further 'solutions' will be reflections or rotations of one of these 13.
Making the 20-unit shape more spread out just increases the simplicity, but does decrease the number of solutions. The puzzle is still trivial. What about a puzzle where the target shape isn't specified? What about if we imagine that we have more pieces!! The puzzle immediately becomes larger, and hence, more complex. Suppose we imagine that we have an F pentomino, and that we have to position the five tetrominoes so that they are still contiguous, but also each edge of each of the 5 squares making the F pentomino is touching a tetromino. We are still only using just 5 tetrominoes, but we are trying to fit them together to form a much more complex shape.
If I gave you any of the above three shapes as a target shape, to be covered by tetrominoes, they would all be very easy, but by not specifying the exact target shape, we have a much better puzzle. Note that examples 1 and 3 are contiguous, but the recreational maths fly can't walk fully around the perimeter of the F without jumping over a corner to corner gap. Peter Esser calculated that over 47,000 different shapes can be made by joining the five tetrominoes together to form 20-ominoes. We now have lots of new puzzles, without having to remember any obscure shapes. Simply take the tetrominoes and surround each of the 12 pentominoes in turn. Also try and surround an additional copy of each of the tetrominoes in turn.
Another challenge? It is trivial to create the longest 20-omino by joining the 5 tetrominoes end to end. A linear length of 15 units is easily found. This can have a minimum width of just two units. (Top diagram below.) Therefore this shape will fit inside a 15x2 rectangle, equalling 30 units. Minor adjustments (diagram two below) changes the width to 4 units, giving a total unit area of 15x4, or 60 units. What is the largest rectangle needed to contain your 20-omino? I've just managed 9x11 or 99. Can that be beaten? Probably.
Finally I would like to hear from any of my readers who can contribute further ideas to increase the popularity of THE TETROMINOES!!!! If I have enthused you to want to try some of these puzzles, you deserve your own set. Here they are. (Coming Oct 2006) Ideally print them on thin card. Bring your own scissors, paper knife, small gnawing animal... |
||||||||||||||||||||||||||||||||||||
|
|
| [Homepage] [What We've Been Up To] [About Me & Al] [Teddington] [Pictures] [Puzzles] [Puzzles Too] [Conversion Kits] [Classics] [Modern Classics] [Desert Island Puzzles] [Coffee Table Puzzles] [Influences] [POV-Ray] [Tetrominoes] [Rec Maths] [Sale & Trade] [Free Puzzles] [Architectural Impossibilities] [Music] [Misc] [My Films] [Credits etc] |
 |
|
|
|

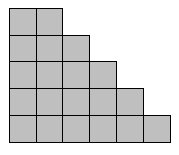
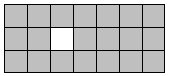
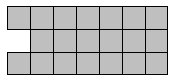
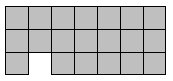
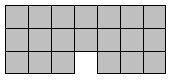
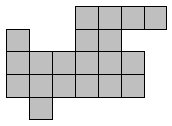 A few minutes' play will quickly show that these problems are trivial to all. Regular shapes with the 5 pieces are few. What about irregular shapes? This shape to the right has three solutions, but it is immediately clear that only one of two pieces can fit in the top right corner, and then the solution quickly becomes too obvious.
A few minutes' play will quickly show that these problems are trivial to all. Regular shapes with the 5 pieces are few. What about irregular shapes? This shape to the right has three solutions, but it is immediately clear that only one of two pieces can fit in the top right corner, and then the solution quickly becomes too obvious.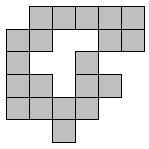

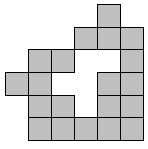

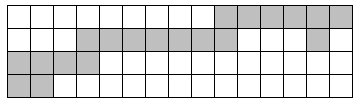
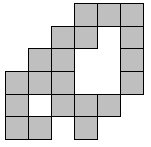 If we pretend that these tetrominoes are very large and very high, we would need to put a fence around the edge!! We would also need to put a fence around any internal holes. What is the maximum number of unit fences that we can require?
If we pretend that these tetrominoes are very large and very high, we would need to put a fence around the edge!! We would also need to put a fence around any internal holes. What is the maximum number of unit fences that we can require?